Zseniális találmányok – Innovatív ötletek: Epizódok az ókori technika történetéből c. virtuális kiállításunk hetedik részében a római matematika rejtelmeiben mélyülünk el!
Az ókori épületek és műszaki létesítmények tervezőinek és kivitelezőinek egyszerű eszközök álltak rendelkezésére. Vázlatokat, mérési adatokat viasztáblára karcoltak be egy hegyes végű bronz pálcikával, az ún. stilusszal. Utóbbiból Aquincumban is több példányt ismerünk. Viasztábla töredéke Budapesten a mai Vörösvári úton, az egykori katonaváros szélén egy kútból, valamint a Bécsi úton, a katonaváros temetőjének egyik sírjából került elő. A terveket feltételezhetően pergamenre rajzolták. A tervezésnél bronzkörzőt használtak, ebből Aquincumban eddig hármat találtak. Kettő szintén sírmellékletként maradt ránk, a harmadik a polgárvárosi Symphorus Mithras szentélyből került elő. Egyenes, derékszög és 45 fok megrajzolására, szerkesztésére bronzból öntött vonalzó és szögmérő állt rendelkezésre, egy ilyet a Szél utcai, ácsszerszámokat tartalmazó leletegyüttesből ismerünk. Függőlegest függőón és függőónos szintező segítségével tudtak beállítani. Eredeti darabokat a Zseniális találmányok – Innovatív ötletek című kiállításon és a Látványtár állandó tárlatán is láthatunk az Aquincumi Múzeumban.

1. kép: Római „mérnök” elképzelt íróasztala viasztáblákkal, stilusszal (írópálcával), vonalzóval, függőónnal, körzővel (Fotó: Szilágyi Nóra)
Mind a műszaki létesítmények tervezésénél, mind a kivitelezésénél, de a vízfogyasztás elszámolásánál, sőt a könyvelőknél és a kereskedőknél is, egyszóval az élet sok területén számolni kellett. A rómaiak görög eredetű szóval abacusnak nevezett számolótáblával számoltak. Az abacus jelentett asztalt, táblát, játéktáblát is. A számolótáblán eredetileg kis kerek kavicsokkal, a calculusokkal (calculi) számoltak. Hérodotosz egy megjegyzése szerint a görögök, sőt az egyiptomiak is kövecskékkel számoltak. A legrégibb görög abakusz, egy vésett márványtábla, 1846-ban Szalamisz szigeténél került elő és feltételezhetően Kr. e. 300 körüli időkből származik. A római korból jelenleg öt abakuszt ismerünk. Egyet Párizsban, egyet Rómában őriznek – sajnos ezek lelőhelye ismeretlen – egy harmadik pedig ásatás során Észak-Olaszországban, a mai Aosta, az ókori Augusta Praetoria városának egyik temetőjéből került elő. Utóbbi tintatartóval és stilusokkal együtt egy hamvasztásos sír melléklete volt és a Kr. u. 1. század végére keltezhető. Ezek bronzból készült, kisméretű (12×8 cm körüli) „zsebszámológépek” voltak. Újkori leírásokból további két darabról van tudomásunk, melyek a 17. században augsburgi és római tudósok magángyűjteményéhez tartoztak, de további sorsuk ismeretlen. Az Aquincumi Múzeum Zseniális találmányok – Innovatív ötletek című kiállítására a Párizsban őrzött példány (őrzési helye: Médailles et Antiques de la Bibliothèque nationale de France) nyomán készítettünk bronzból egy rekonstrukciót, mely a kiállításon megtekinthető.
1. videó: Római minta alapján készített abakusz használata
A római abakusz
A római számolótáblák téglalap alakúak. A tábla felső részén nyolc rövid, a tábla alsó részén a fennmaradt példányokon kilenc hosszú vájat van. A csak leírásból ismert augsburgi és római abakuszokon a kilencedik vájat helyett a tábla jobb szélen egymás alatt három rövidebb hornyolat lehetett. A felső és az alsó vájatsor között vannak jelölve a számértékek. Balról jobbra az első hét jelölés és annak kifejezése arab számmal a következő:
IXI = 1.000.000 (decies centena milia)
(((I))) = 100.000 (centum milia)
((I)) = 10.000 (decem milia)
(I) = 1.000 (mille)
C = 100 (centum)
X = 10 (decem)
I = 1 (unus)
A nyolcadik alsó és felső vájat között a görög théta betű szerepel, ami az egész 1/12 részének, azaz az uncianak a jelölésére szolgál. A legutolsó vájatban vagy vájatokban pedig a fél, a negyed- és a harmad-uncia (azaz az 1/24, 1/48 és 1/36) számolható.
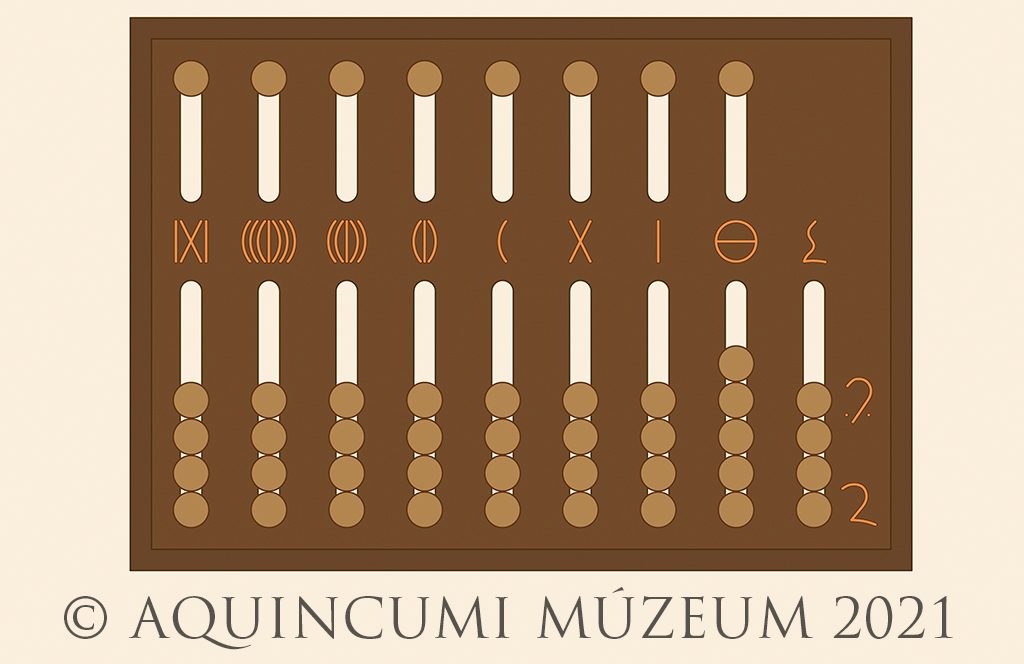
2. kép: A római abakusz szerkezete (Rajz: Lajtos Tamás)
A római számolótáblákkal 9.999.999-ig tudjuk ábrázolni az egész számokat, az utolsó két vájatban pedig a törteket. A vájatokba kis bronz gömböcskéket, számológolyókat illesztettek be, ezek jelentik 1-től 9-ig a számjegyeket. Az alsó vájatokban egyenként négy golyó van, ezek mindegyikének értéke 1. A felsőkben egy golyó van, amelynek értéke 5. Balról a nyolcadik alsó vájatban öt golyó van, ezek mindegyikének értéke az egész 1/12 része, azaz egy uncia. A nyolcadik felső vájatban egy golyó található, melynek értéke 6 uncia (az egész 6/12 része). Az utolsó, azaz jobb szélső vájatban a tört unciákat lehet számolni. Itt négy számológolyót találunk. A felső értéke fél uncia, azaz az egész 1/24 része. A következő golyó értéke egynegyed uncia, azaz az egész 1/48 része. Az alsó két golyó egyenként egyharmad uncia értékű, azaz az egész 1/36-1/36 része. Mivel 1/24 meg 1/24 az már 1/12, vagyis egy uncia, azt balra a következő vájatban lehet már jelölni. Ugyanígy a negyed unciát jelölő számológolyóból csak egy van, mert két negyed uncia, az egy fél uncia, ami a következő, felső számológolyó értéke. A harmadunciás számológolyóból kettő kell, mert 1/36 meg 1/36 az 2/36, amit másik számológolyó nem jelöl.
Legyél te az ókor mérnöke!
Számoljunk a római abakusszal!
A római számolótáblák igazából a fejben számolás követésére szolgáltak. Segítségükkel összeadni, kivonni és szorozni lehetett. Alaphelyzetben az alsó vájatokban ülő golyók le, a felsőkben ülők fel vannak húzva. Azokat az értékeket, amikkel számolunk, középre húzzuk. Nézzünk egy egyszerű számolást. 625-höz adjuk hozzá a 127-t! Először állítsuk be az abakuszon a 625-t! Ezután jobbról balra haladva először az egyeseket adjuk össze és ábrázoljuk a számolótáblán, majd a tízeseket, végül a százasokat. Az eredmény 752. A következő kisfilm ennek római abakusszal való kiszámolását mutatja:
2. film Összeadás a római abakusszal
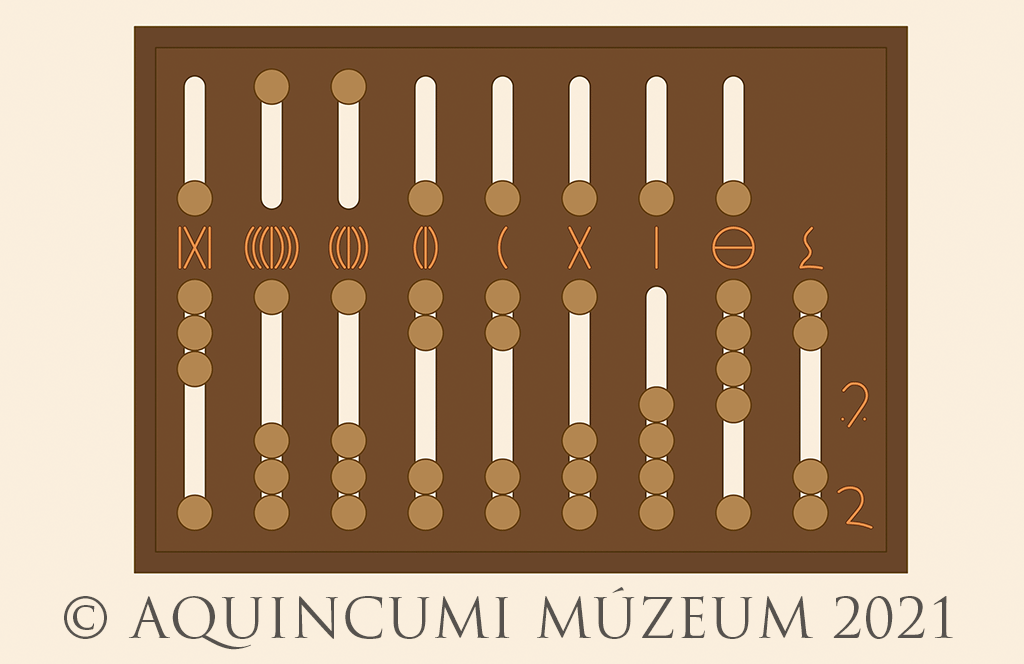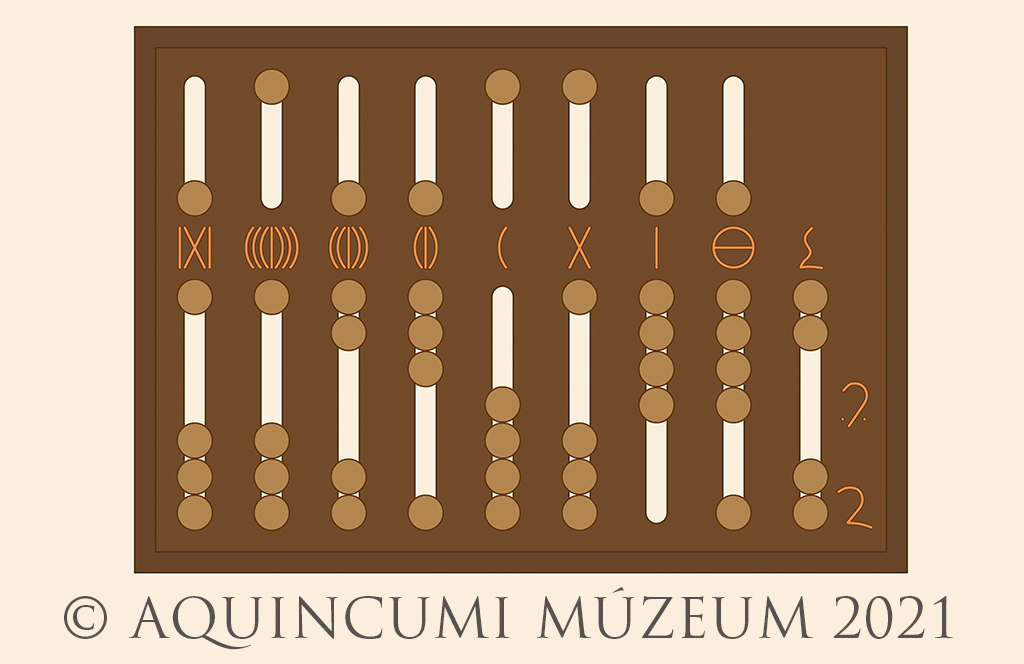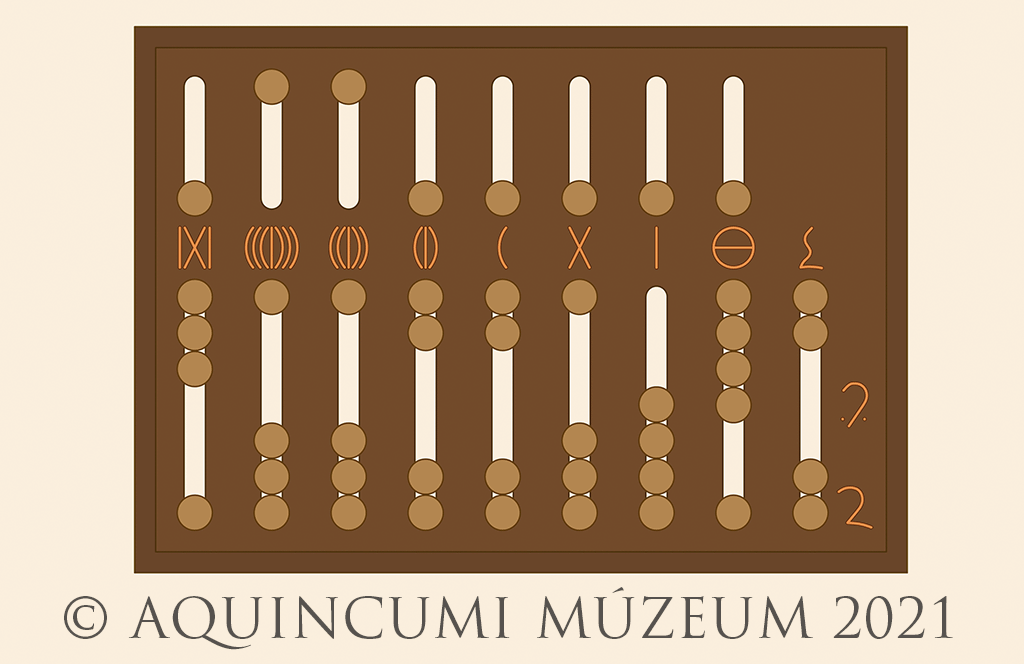
Vegyünk egy nagyobb számot! A következő képen jelölt szám a 6.178.019, valamint tíz uncia (10/12), továbbá egy fél (1/24) és egy negyed uncia (1/48):
3a. kép: 6.178.019, valamint 43/48 ábrázolása az abacuson (Rajz: Lajtos Tamás, szerkesztette Kolozsvári Krisztián)
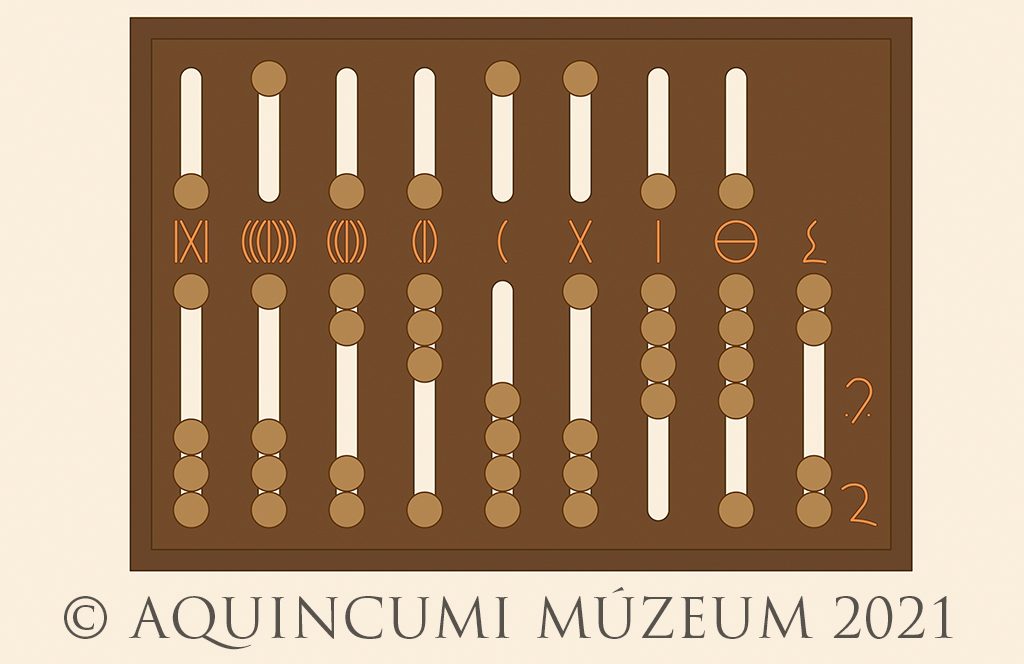
3b. kép: 6.178.019, valamint 43/48 (Rajz: Lajtos Tamás)
Az előbb ábrázolt számhoz adjunk hozzá 1.939.746-ot. A végeredmény a 4. képen leolvasható az abakuszról, mégpedig arab számokkal kifejezve 8.117.765 és 43/48.
4. kép: Az összeadás és az eredmény: 8.117.765 és 43/48 (Rajz: Lajtos Tamás, szerkesztette: Kolozsvári Krisztián)
Kivonás esetében vonjuk ki egymásból az egyeseket, tízeseket, százasokat és így tovább, a részeredményeket állítsuk be az abakuszon, a végeredmény a számoló tábláról leolvasható.
3. videó: Kivonás a római abakuszon
Ha nagyobb, például háromjegyű arab számokat szeretnénk a római abakuszon összeszorozni, akkor bontsuk le a számokat százasokra, tízesekre, egyesekre, ezeket egyenként szorozzuk össze egymással, és adjuk össze. Az abakuszon követhetjük a részeredményeket, amíg megkapjuk a végeredményt. Például 428×111 az:
400×100=40000
20×100=2000+40000=42000
8×100=800+42000=42800
400×10=4000+42800=46800
20×10=200+46800=47000
8×10=80+47000=47080
400×1=400+47080=47480
20×1=20+47480=47500
8×1=8+47500=47508
4. videó: Szorzás római abakusszal
De hogyan osztottak a rómaiak? Ezt nem tudjuk. J. Hilton Turner javaslata szerint (Roman elementary mathematics. The Classical Journal 47, 1951, 63-74, 106-108) a következőképpen oszthattak:
808-at osszunk el 35-tel:
808-ban a 35 biztosan megvan 10-szer, marad a 458.
458-ban a 35 biztosan megvan 10-szer, marad a 108.
108-ban a 35 biztosan megvan egyszer, marad a 73.
73-ban a 35 biztosan megvan egyszer, marad a 38.
38-ban a 35 biztosan megvan egyszer, marad a 3.
Azaz 808-ban a 35 megvan 23-szor és az abakuszon marad 3.
Írta: Dr. Fényes Gabriella
Virtuális kiállításunk előző részei ide kattintva érhetők el.